 大家在备考的时候,尤其面对着让人头疼的数量关系题目,会不会有这样的疑问:为什么别人看到题目就马上有思路,而我和题目“干瞪眼”五分钟,也不知从何下手。同学们也不用着急,这是因为大家没有找到备考的重点,没有形成面对解题的系统思路,今天老师就给大家介绍一种,解决工程问题的固定套路----“三步走”。(文章后面给大家准备了思维导图,大家要记得及时保存啊!)
大家在备考的时候,尤其面对着让人头疼的数量关系题目,会不会有这样的疑问:为什么别人看到题目就马上有思路,而我和题目“干瞪眼”五分钟,也不知从何下手。同学们也不用着急,这是因为大家没有找到备考的重点,没有形成面对解题的系统思路,今天老师就给大家介绍一种,解决工程问题的固定套路----“三步走”。(文章后面给大家准备了思维导图,大家要记得及时保存啊!)
一、题型特征
以前通常把修桥、铺路以及明显涉及工程量的问题看成工程问题,但现在我们通常把完成一件事情需要多长时间的问题看成工程问题。
工程问题的核心公式为工作总量=工作效率×工作时间。
例如:社区小李录入一组数据,检测样本总数为3000份,工作时间为12小时,平均每小时录入数据为250份。那么样本总数3000份就是工作总量,12小时就是工作时间,250份/小时就是工作效率。
二、固定套路----“三步走”
(一)给定时间型
【特征】题目中给出不同主体的工作时间,问的时间。
【步骤】1.赋值总量----赋值总量为时间的公倍数
2.算出效率
3.再去求解
大家一起来做道题:
【例1】一项工程由甲、乙工程队单独完成,分别需50天和80天。若甲、乙工程队合作20天后,剩余工程量由乙、丙工程队合作需12天完成,则丙工程队单独完成此项工程所需的时间是:
A. 40天 B. 45天
C. 50天 D. 60天
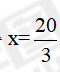
【解析】通过题干中给定甲、乙单独做工的时间,最后问的时间,先判断本题是时间类工程问题。赋值工作总量为50和80的最小公倍数400,计算出甲的工作效率为8,乙的工作效率为5。设丙的工作效率为x,根据题意可得20×(8+5)+12×(5+x)=400,解得,则丙单独完成所需的时间为400÷=60(天)。因此,选择D选项。
例1是工程问题中的时间类考题,通过设工作量为多个时间的公倍数,再分别计算出效率。
(二)效率制约型
【特征】当题目中不仅给定工作时间,还给出与效率相关的关系。
【步骤】1.赋值效率----按照比例关系赋值
2.算出总量
3.再去求解
【例2】甲、乙、丙工作效率的比例为3∶4∶5,甲单独做A工程需要25天,丙单独做B工程需要9天,现甲乙丙合作两项工程,一共需要( )天。
A. 8 B. 9
C. 10 D. 11
【解析】根据“甲、乙、丙工作效率的比例为3∶4∶5”,赋值甲、乙、丙的效率分别为:3、4、5。根据“甲单独做A工程需要25天”,可知A工程工作总量为3×25=75;根据“丙单独做B工程需要9天”,可知B工程工作总量为5×9=45。A、B两项工程的总工作量为:75+45=120,则甲乙丙合作需要的时间:120÷(3+4+5)=10(天)。
因此,选择C选项。
例2给出效率之间的比例关系和做工时间,是效率类的工程问题,赋值出效率再计算出工作总量。通过上面两道例题,大家是否初步掌握解题技巧了呢!这种工程问题只要能够辨别题目特征,同时掌握基本的赋值方法,解决起来还是很简单的。
公考备考的道路上,唯有“坚持”才会取得最后的胜利,梦想是奋斗出来的,让我们一起努力吧!












