公考中数量关系中的排列组合问题是很多人头疼的问题,不少人表示虽然排列组合在中学学过,但是,当时都听的一知半解,对于其具体原理理解起来比较困难,做题纯凭感觉。其实,在排列组合中有一些方法与技巧可以快速的理解并解决对应的问题,例如“捆绑法”、“插空法”、“隔板法”等。捆绑插空比较常见,大家也对其比较了解了,今天分享一个只要大家理解,套结论就可以得分的插空法。
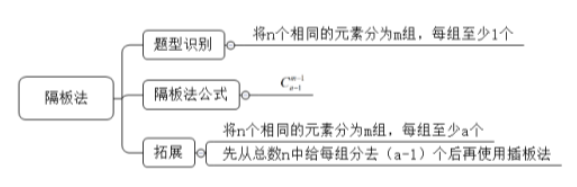
一、题型特点:题干中出现“将n个相同的元素分为m组,每组至少1个”。
![]()
二、解题方法:总情况数:。
解题方法可以理解为先将n个元素排成一列,再将隔板插入到元素间的空隙中,这样就将元素分好组了。n个元素中间有n-1个空隙,分m组需要插入m-1块隔板,完成这个分组就是需要在n-1个空隙中选取m-1个空隙插入隔板,即𝐶𝑛−1𝑚−1。知道了方法,再来看一下具体怎么使用。
三、真题感知
【例1】某城市一条道路上有4个十字路口,每个十字路口至少有一名交通协管员,现将8个协管员名额分配到这4个路口,则每个路口协管员名额的分配方案有:
A.35种 B.70种
C.96种 D.114种
【答案】A
【解析】第一步,本题考查排列组合问题,属于方法技巧类。
![]()
第二步,题干中“将8个协管员名额分配到这4个路口”,是8个名额,也就是8个相同元素。分到4个路口,即分为4组,而且每个路口至少一个名额,符合“隔板法”的使用条件,直接套用公式,。
因此,选择A选项。
前述隔板法的应用条件中有一个限制是每人至少一个,那如果题干问至少2个或者至少3个怎么办呢?下面一起再看一道真题。
【例2】某办公室接到15份公文的处理任务,分配给甲、乙、丙三名工作人员处理。假如每名工作人员处理的公文份数不得少于3份,也不得多于10份,则共有( )种分配方式。
A.15 B.18
C.21 D.28
【答案】D
【解析】第一步,本题考查排列组合问题,属于方法技巧类。
![]()
第二步,需要将15份公文分给三个人,每人至少3份(满足这个条件,每人肯定不多于10份),此处可利用隔板法,既然每个人至少3份,可以先给每人两份,剩下了15-2×3=9(份)。现在题目就转换成了9份公文分给三个人,每人至少1份,可以直接套用隔板法公式。
因此,选择D选项。
三、知识点综述
通过上面两道题可以感受到,能利用隔板法的关键是相同的元素,之所以要求是相同元素,是由于只有在不考虑被分配的元素顺序的情况下,才能用上述方法求解。若要考虑顺序就不能简单的利用隔板法来求,比如若将例1中的名额改为人,做法就不一样了。在利用隔板法时一定要注意使用条件,同时也要兼顾灵
活性。类似例2的方法,我们要学会举一反三,若题目中出现至少2个,我们就先给每组先分1个,再将剩下的相同元素用隔板法的公式进行分配。所以下次变成至少a个,我们就先从总数中给每组先分去(a-1)个,再用隔板法的公式求解即可。大家可以通过下面的思维导图再巩固下“隔板法”这个知识点。