公职考试时间紧,任务重,所以要想在短时间内拿下,必须要掌握一定的方法,本文就带着各位考生学习一个可以套用模型解题的题型,那就是排列组合里面的隔板模型,先来了解一下什么题中可以用隔板模型。
一、应用环境
当题干中出现了n个相同元素分给m个不同的对象,每个对象至少分1个,问有多少种方法,那么这就属于隔板模型,

二、基本应用
例1:公司采购了一批新的同一类型的电脑共8台,计划分给公司的3个部门,每个公司至少分一台,最终电脑全部分完,共有多少种不同的分配方案?
A.19 B.20 C.21 D.22
【解析】此题满足隔板模型的所有条件,相当于把8个相同元素“电脑”分给3个不同对象“部门”,且每个部门至少分到了一个,故直接套用公式,

二、基本应用
例1:公司采购了一批新的同一类型的电脑共8台,计划分给公司的3个部门,每个公司至少分一台,最终电脑全部分完,共有多少种不同的分配方案?
A.19 B.20 C.21 D.22
【解析】此题满足隔板模型的所有条件,相当于把8个相同元素“电脑”分给3个不同对象“部门”,且每个部门至少分到了一个,故直接套用公式,
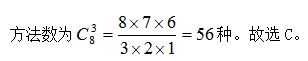
例3:老师决定将10个足球分给4个同学,但是还没想好怎么分,那么这个老师共有多少种不同的分法?
A.286 B.276 C.56 D.72
【解析】:此题目也属于相同元素的不同分堆,那么如何使其为满足公式基本条件。可以先从每个同学那里借一支铅笔,此时老师有14支铅笔,并且欠了每个同学一支铅笔,在分发的时候,必须至少给每个同学一支。那么即可满足将14支铅笔分给4个同学,每个同学至少分一支,
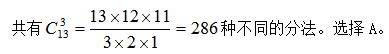
四、实战应用
例4:某部门购买了30本笔记本,发给了3组,每组至少发9本。那么,一共有( )种发放方法?
A.10 B.17 C.14 D.15
【解析】:隔板模型标准题型为“每人至少分1个”,题目中为“每人至少分9个”,因此不能直接代入公式,需要先转化为标准题型,先给3个组每组分配8本书,还剩30-24=6本书,此时本题转换为“6本笔记本分配到3个组,每组至少分1本”,此时可以代入隔板模型公式,

通过以上基本例题,希望各位考生可以真正学懂隔板模型,从而利用隔板模型快速解决与之类似的一系列问题,在考试中顺利拿下“一城”。











